Conceptual understanding in education emphasizes grasping underlying principles and ideas, enabling students to apply knowledge flexibly across contexts. Procedural fluency focuses on mastering the steps and techniques necessary to perform tasks accurately and efficiently. Balancing both approaches enhances problem-solving skills and fosters deeper learning outcomes.
Table of Comparison
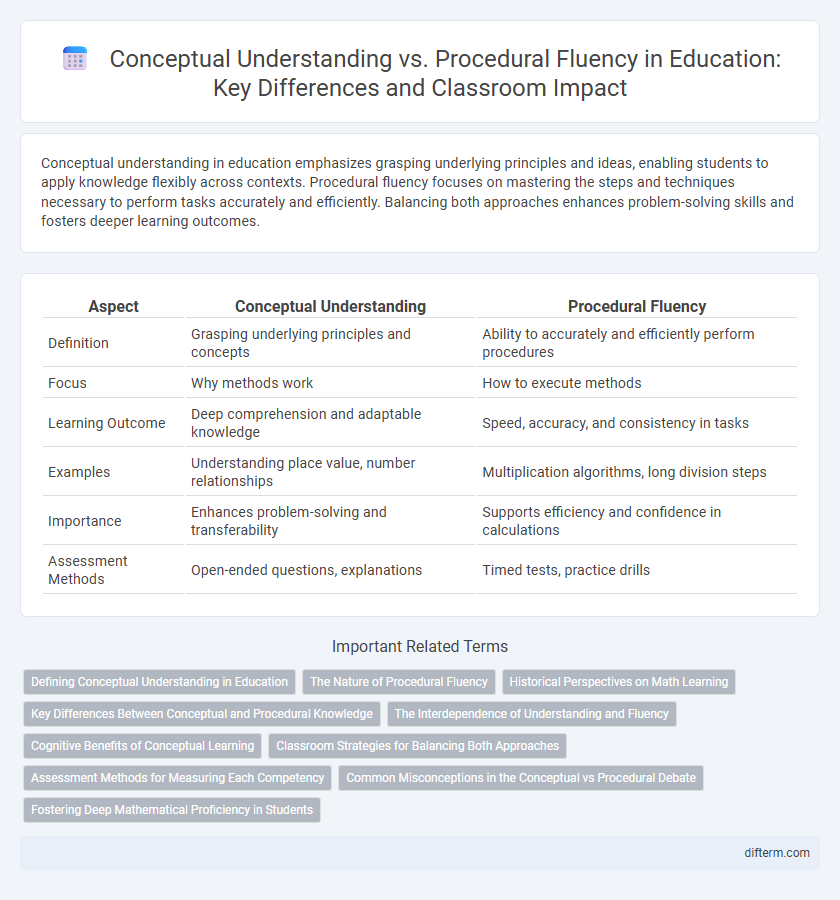
| Aspect | Conceptual Understanding | Procedural Fluency |
|---|---|---|
| Definition | Grasping underlying principles and concepts | Ability to accurately and efficiently perform procedures |
| Focus | Why methods work | How to execute methods |
| Learning Outcome | Deep comprehension and adaptable knowledge | Speed, accuracy, and consistency in tasks |
| Examples | Understanding place value, number relationships | Multiplication algorithms, long division steps |
| Importance | Enhances problem-solving and transferability | Supports efficiency and confidence in calculations |
| Assessment Methods | Open-ended questions, explanations | Timed tests, practice drills |
Defining Conceptual Understanding in Education
Conceptual understanding in education refers to grasping the underlying principles and relationships that connect various ideas within a subject. It enables students to apply knowledge flexibly across different contexts rather than merely memorizing procedures. This deep comprehension fosters critical thinking and problem-solving skills essential for academic success.
The Nature of Procedural Fluency
Procedural fluency involves the ability to apply methods and algorithms efficiently, accurately, and flexibly in various mathematical contexts. It emphasizes skill mastery through practice, enabling students to execute procedures without hesitation and to adapt strategies when solving problems. This contrasts with conceptual understanding, as procedural fluency centers on the consistent performance of mathematical tasks rather than deep insight into the underlying concepts.
Historical Perspectives on Math Learning
Historical perspectives on math learning reveal ongoing debates between prioritizing conceptual understanding and procedural fluency. Early 20th-century education often emphasized rote memorization and algorithmic proficiency, while later research by cognitive psychologists highlighted the importance of deep conceptual frameworks for long-term retention. Contemporary pedagogy integrates both approaches, recognizing that robust math education requires balancing procedural skills with comprehensive conceptual insights.
Key Differences Between Conceptual and Procedural Knowledge
Conceptual understanding involves grasping the underlying principles and relationships that form the foundation of knowledge, enabling flexible problem-solving across contexts. Procedural fluency refers to the ability to accurately and efficiently execute specific methods or algorithms through practice and repetition. Key differences include conceptual knowledge promoting depth and adaptability, while procedural fluency emphasizes speed and accuracy in applying learned procedures.
The Interdependence of Understanding and Fluency
Conceptual understanding and procedural fluency are deeply interconnected, as strong conceptual understanding enables learners to grasp the underlying principles behind methods, supporting flexible application. Procedural fluency reinforces conceptual understanding by providing practice that solidifies knowledge and promotes efficiency in problem-solving. Balancing both elements enhances overall mathematical competence, leading to improved critical thinking and adaptive learning.
Cognitive Benefits of Conceptual Learning
Conceptual learning enhances deep cognitive processing by fostering meaningful connections between ideas, which improves long-term retention and transferability of knowledge. It strengthens critical thinking and problem-solving skills by encouraging learners to understand underlying principles rather than just memorizing steps. This foundational understanding supports adaptive expertise, enabling students to apply knowledge flexibly across various contexts.
Classroom Strategies for Balancing Both Approaches
Classroom strategies for balancing conceptual understanding and procedural fluency include incorporating hands-on activities that allow students to explore mathematical concepts deeply while practicing step-by-step problem-solving techniques. Using formative assessments helps teachers identify gaps in either conceptual knowledge or procedural skills, enabling targeted interventions that foster both cognitive processes. Differentiated instruction, such as mixing direct instruction with inquiry-based learning, ensures students develop a robust grasp of underlying principles alongside efficient procedure mastery.
Assessment Methods for Measuring Each Competency
Assessment methods for conceptual understanding in education often involve open-ended questions, reflective essays, and problem-solving tasks that require explanation of underlying principles. Procedural fluency is typically measured through timed tests, step-by-step problem-solving exercises, and repetitive drills that assess accuracy and speed in executing specific procedures. Combining formative assessments with performance tasks ensures a comprehensive evaluation of both conceptual grasp and procedural skills.
Common Misconceptions in the Conceptual vs Procedural Debate
Common misconceptions in the conceptual versus procedural fluency debate often revolve around the false dichotomy that one must prioritize either deep understanding or efficient skill execution exclusively. Research indicates that integrating conceptual understanding with procedural fluency creates more robust learning outcomes than focusing solely on memorizing steps or abstract concepts. Educators should emphasize the symbiotic nature of these two domains to avoid undermining either aspect of mathematical competence.
Fostering Deep Mathematical Proficiency in Students
Fostering deep mathematical proficiency in students requires balancing conceptual understanding with procedural fluency to enable flexible problem solving and critical thinking. Emphasizing conceptual understanding helps students grasp underlying mathematical principles, while procedural fluency ensures efficient and accurate execution of algorithms. Integrating both approaches supports long-term retention and the ability to apply mathematics in varied contexts, enhancing overall mathematical competence.
conceptual understanding vs procedural fluency Infographic
 difterm.com
difterm.com